最小二乗法による近似直線の係数を行列計算で求める方法
最小二乗法を使って近似直線を引くには、行列計算を使うと考え方が簡単です。
まず準備運動として、平面上の2点![]() を通る直線
を通る直線![]() を引いてみましょう。このとき、
を引いてみましょう。このとき、
![]()
とおけば、
![]()
と書けます。よって、
![]()
と表すことができます。求めたい![]() ベクトルは、左から
ベクトルは、左から![]() の逆行列をかけて、
の逆行列をかけて、
![]()
とすれば求まります。ここまでは問題ありませんよね?
最小二乗法を使う場合は、点の数が3点以上になる場合であって、
![Rendered by QuickLaTeX.com $$ Y=\left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right], X=\left[\begin{array}{cc} x_1 & 1 \\ x_2 & 1 \\ \vdots & \vdots \\ x_n & 1 \end{array}\right], A=\left[\begin{array}{c} a \\ b \end{array}\right], \, \left(n \geq 3\right) $$](https://miscellaneous.tokyo/wp-content/ql-cache/quicklatex.com-45799ab89f032338de00cec74e83e5f5_l3.png)
として、
![]()
と書くことができます(直線が必ずしもすべての点を通らないのでニアリイコールを使っています)。でも、![]() が正方行列ではないので、逆行列を求めることができません。
が正方行列ではないので、逆行列を求めることができません。
ところが、左から転置行列をかけてしまえば、正方行列になるではありませんか。
つまり、
![]()
とすれば、![]() は
は![]() の行列で、
の行列で、![]() が
が![]() の行列なので、
の行列なので、![]() は
は![]() の正方行列になります。
の正方行列になります。
この正方行列が正則であれば、逆行列が存在します。それを左から掛けると、
![]()
となり、何かしらの![]() が解析的に求まるではありませんか!
が解析的に求まるではありませんか!
実は、これが最小二乗法で求めた解と一致するのです。
何と素晴らしい!
ちなみに、ここでは、![]() の2次元平面について述べていますが、3次元以上の多次元でも同様に考えることができます。
の2次元平面について述べていますが、3次元以上の多次元でも同様に考えることができます。
念のため、実データで検算してみる
行列を使わずに係数を求めた前回の記事で使ったデータ![]() で検算してみます。この答えは
で検算してみます。この答えは![]() でした。
でした。
まず、データから配列を作ります。
![Rendered by QuickLaTeX.com $$ Y=\left[\begin{array}{r} -6 \\ 3 \\ 0 \end{array}\right], X=\left[\begin{array}{rr} -2 & 1\\ 1 & 1 \\ 4 & 1 \end{array}\right] $$](https://miscellaneous.tokyo/wp-content/ql-cache/quicklatex.com-8f5da8954f2122b829562150e1d7960f_l3.png)
よって、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\begin{array}{r} a \\ b \end{array}\right] &=&\left( X^\mathsf{T} X \right)^{-1} X^\mathsf{T} Y \\ &=&\left( \left[\begin{array}{rrr} -2 & 1 & 4\\ 1 & 1 & 1 \end{array}\right] \left[\begin{array}{rrr} -2 & 1 \\ 1 & 1 \\ 4 & 1 \end{array}\right] \right)^{-1} \left[\begin{array}{rrr} -2 & 1 & 4\\ 1 & 1 & 1 \end{array}\right] \left[\begin{array}{r} -6 \\ 3 \\ 0 \end{array}\right] \\ &=& \left[\begin{array}{rr} 21 & 3\\ 3 & 3 \end{array}\right]^{-1} \left[\begin{array}{r} 15 \\ -3 \end{array}\right]\\ &=&\frac{1}{54} \left[\begin{array}{rrr} 3 & -3 \\ -3 & 21 \end{array}\right] \left[\begin{array}{r} 15 \\ -3 \end{array}\right] \\ &=&\frac{1}{54} \left[\begin{array}{r} 54 \\ -108\end{array}\right] \\ &=&\left[\begin{array}{r} 1 \\ -2\end{array}\right] \end{eqnarray*}](https://miscellaneous.tokyo/wp-content/ql-cache/quicklatex.com-7e2fc8b4bd6860d0e9b66a05eb16af8a_l3.png)
となり、あらかじめ示しておいた答えと一致しました。
証明
念のため、証明します。
まず、誤差の二乗和![]() を考えます。
を考えます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} E &=& \sum_{i=1}^{n}\left\{y_i -\left(a x_i + b\right)\right\}^{2} \\ &=& \left(\left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right]- \left[\begin{array}{cc} x_1 & 1 \\ x_2 & 1 \\ \vdots & \vdots \\ x_n & 1 \end{array}\right] \left[\begin{array}{c} a \\ b \end{array}\right] \right)^\mathsf{T} \left(\left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right]- \left[\begin{array}{cc} x_1 & 1 \\ x_2 & 1 \\ \vdots & \vdots \\ x_n & 1 \end{array}\right] \left[\begin{array}{c} a \\ b \end{array}\right] \right)\end{eqnarray*}](https://miscellaneous.tokyo/wp-content/ql-cache/quicklatex.com-442ca866dd559255a2b094d044a51e48_l3.png)
ここで、
![Rendered by QuickLaTeX.com $$ Y=\left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right], X=\left[\begin{array}{cc} x_1 & 1 \\ x_2 & 1 \\ \vdots & \vdots \\ x_n & 1 \end{array}\right], A=\left[\begin{array}{c} a \\ b \end{array}\right] $$](https://miscellaneous.tokyo/wp-content/ql-cache/quicklatex.com-18f731b290dc19ba3864f0bb14cafa56_l3.png)
とおくと、
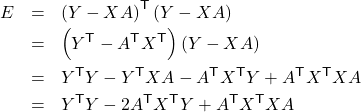
となります。ただし、最後の式変形では、
![]()
であることを使いました。![]() は、
は、![]() 、
、![]() 、
、![]() の行列の積なのでスカラ値であり、転置をとっても値が変わりません。
の行列の積なのでスカラ値であり、転置をとっても値が変わりません。
ここで、
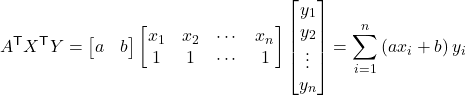
および

であることに注意して、![]() を
を![]() それぞれで偏微分して、勾配ベクトルを求めると、
それぞれで偏微分して、勾配ベクトルを求めると、

となります。
誤差の二乗和が最小値になる条件は、この勾配ベクトルが0になるときで、
![]()
です。これは、(1)に示した条件になるので、(2)で係数が計算できることが示されました。




コメント