高周波回路を設計していると、マッチングを取る等、インピーダンスを変換したい場面が出てきます。あなたは、![]() と
と![]() のインピーダンス変換をするためには、特性インピーダンスが
のインピーダンス変換をするためには、特性インピーダンスが![]() で、長さが
で、長さが![]() 変成器を使えばよいということをご存じのことでしょう。ただ、その原理を考えたことがありますでしょうか?
変成器を使えばよいということをご存じのことでしょう。ただ、その原理を考えたことがありますでしょうか?
インピーダンス変換ができる理由
特性インピーダンスが![]() のスミスチャートを考えます。
のスミスチャートを考えます。
このスミスチャート上に、![]() (スミスチャート上にプロットすると
(スミスチャート上にプロットすると![]() )とは異なるインピーダンス
)とは異なるインピーダンス![]() (同
(同![]() )をとります。
)をとります。
この![]() を、特性インピーダンスが
を、特性インピーダンスが![]() で長さが
で長さが![]() の伝送線路を介して見ると、前回の記事に示したように、
の伝送線路を介して見ると、前回の記事に示したように、![]() を中心にして時計回りに半周回ったところに写像され、
を中心にして時計回りに半周回ったところに写像され、![]() (
(![]() )になります。
)になります。
また、![]() から考えても同様に
から考えても同様に![]() になります。
になります。
つまり、![]() と
と![]() は、
は、![]() の
の![]() 変成器で相互にインピーダンス変換されることになります。
変成器で相互にインピーダンス変換されることになります。
ここで、![]() 、
、![]() 、
、![]() はどのような関係になるでしょうか?
はどのような関係になるでしょうか?
まず、インピーダンスと反射の関係から、
![]()
及び
![]()
です。また、スミスチャートは![]() が原点であり、
が原点であり、![]() と
と![]() は符号を入れ替えた関係になるので、
は符号を入れ替えた関係になるので、
![]()
です。これらを連立させると、
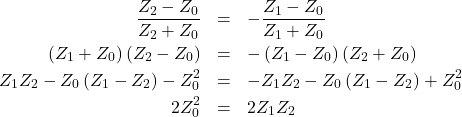
となります。よって、
![]()
です。
Z1、Z2は複素数でも成り立つ
図では、![]() 、
、![]() をたまたま実軸上に取りました。しかし、結果として得られた相乗平均を導くとき、
をたまたま実軸上に取りました。しかし、結果として得られた相乗平均を導くとき、![]() 、
、![]() が実数であることを要求してはいません。すなわち、複素数でも成り立ちます。
が実数であることを要求してはいません。すなわち、複素数でも成り立ちます。
ただ、複素数の特性インピーダンスという話を聞いたことがないので、積である![]() は正の実数になる必要があります。
は正の実数になる必要があります。
ここで、![]() 、
、![]() を非負の実数、
を非負の実数、![]() 、
、![]() を実数として、
を実数として、
![]()
及び、
![]()
とおくと、
![]()
なので、
![]()
を満たせば、
![]()
なる特性インピーダンスで、長さが![]() の伝送線路によって相互にインピーダンス変換をすることができます。
の伝送線路によって相互にインピーダンス変換をすることができます。
特別な場合1
特別な場合として、![]() 、
、![]() を考えます。
を考えます。![]() は明らかです。
は明らかです。
このとき、![]() 、
、![]() となり、抵抗性のインピーダンス同士であれば、
となり、抵抗性のインピーダンス同士であれば、![]() の
の![]() 線路で必ずインピーダンス変換ができます。
線路で必ずインピーダンス変換ができます。
特別な場合2
別の特別な場合として、![]() 、
、![]() を考えます。
を考えます。![]() は明らかです。
は明らかです。
このとき、![]() 、
、![]() となり、符号の異なるリアクタンス同士であれば、
となり、符号の異なるリアクタンス同士であれば、![]() の
の![]() 線路で必ずインピーダンス変換ができます。
線路で必ずインピーダンス変換ができます。
特別な場合3
更に別の特別な場合として、![]() 、
、![]() を考えます。
を考えます。![]() は明らかです。
は明らかです。
このとき、![]() 、
、![]() となり、共役複素数の関係です。これらは、
となり、共役複素数の関係です。これらは、![]() の
の![]() 線路でインピーダンス変換ができます。
線路でインピーダンス変換ができます。
ブランチラインの解析ではこの理論を使います。
具体例
具体例1
![]() を
を![]() 、
、![]() を
を![]() とすると、
とすると、
![]()
となり、約![]() の
の![]() の伝送線路で相互にインピーダンス変換ができます。
の伝送線路で相互にインピーダンス変換ができます。
具体例2
![]() を
を![]() 、
、![]() を
を![]() とすると、
とすると、
![]()
となり、約![]() の
の![]() の伝送線路で相互にインピーダンス変換ができます。
の伝送線路で相互にインピーダンス変換ができます。
まとめ
スミスチャートの特性インピーダンス![]() を
を![]() に捕らわれることなく考えることが肝要です。
に捕らわれることなく考えることが肝要です。
![]() を見ると条件反射的に
を見ると条件反射的に![]() と考えてしまう方にとっては、コロンブスの卵的な考え方だと思います。
と考えてしまう方にとっては、コロンブスの卵的な考え方だと思います。





コメント
よくわからなかったので教えてください。
ZoをZ1とZ2を結ぶ線分の中心に設定すれば良いと理解しました。
Zoが実数の時はなんとなく理解できるのですが、複素数の時はどのような線路になるかわからなかったので教えていただきたいです。
このや様、ご質問をありがとうございます。
本記事中で、「複素数の特性インピーダンスという話を聞いたことがないので、積であるZ1Z2は正の実数になる必要があります。」として、Z0(特性インピーダンス)を実数に限定し、複素数の場合から逃げていたつもりでした。
このや様からご質問をいただいて、改めて「伝送線路の特性インピーダンスが√(L/C)、伝搬速度が1/√(LC)と近似できることを導いてみた」という記事の式(11)を見直してみると、伝送線路に抵抗分(R)かコンダクタンス分(G)があれば、複素成分が出現することが分かりました。よって、導電率の悪い金属を使うか、絶縁抵抗の低い誘電体を使うこと等によって、複素数の特性インピーダンスを作ることが可能ということになります。ただ、伝送損失が発生するので、「伝送線路を介して見るインピーダンスがスミスチャート上を時計回りに回る理由」という記事におけるスミスチャートのα>0の場合に示すように、伝送線路の長さに応じてインピーダンスがスミスチャートの中心に近づいてしまいます。よって、現実的にマッチングをとることはなかなか難しいと思います。